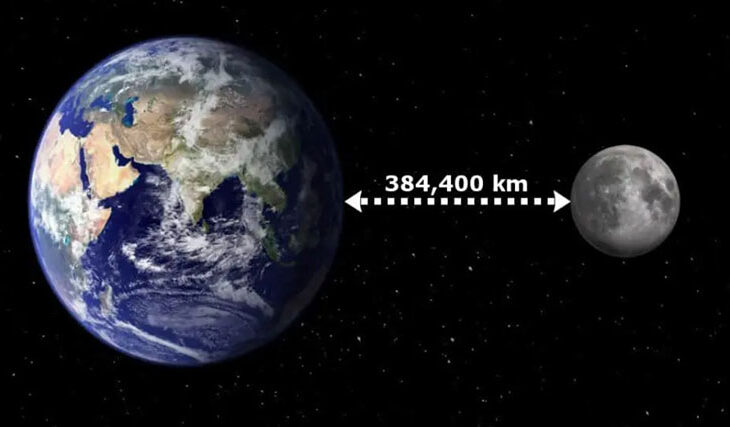
The average distance to the Moon is 384,403 km.
Why “average”?
Because the Moon revolves around the Earth in an elliptical orbit, which means that at some point it will be further, and at some, on the contrary, it will be closer.
When the Moon is at its closest point to the Earth (perigee), we are only 363,104 km apart.
And the distance from the most distant point (apogee) to the Earth is as much as 406,696 km.
It turns out that the distance from the Earth to the Moon varies within 43,592 km.
Due to this rather large difference, the moon in the night sky is of different sizes. At perigee, the Moon looks 15% larger to us than at apogee.
The difference in distances also affects the brightness of the Moon when it reaches its full phase. At the point closest to the Earth, the full moon is usually 30% brighter than at its maximum distance from our planet. When the full moon is at perigee, it is called a “supermoon”.
How to determine the distance to the moon?
Calculations of the ancient Greeks
In the work of Aristarchus of Samos “On the magnitudes and distances of the Sun and Moon” (3rd century BC), the first attempt in the history of science to establish the distances to these Moon and Sun is made, as well as to determine their sizes.
Aristarchus proceeded from the assumption that the Moon has the shape of a ball and shines with light reflected from the Sun. In those moments when the Moon has the form of a half-disk, it forms a right triangle with the Earth and the Sun.
If at this moment we accurately determine the angle between the directions from the Earth to the Moon and to the Sun (CAB), we can find from simple geometric relationships how many times the leg (the distance from the Earth to the Moon AB) is less than the hypotenuse (the distance from the Earth to the Sun AC). According to Aristarchus, CAB=87°; therefore, the ratio of these sides is 1:19.
Aristarchus was wrong about 20 times. In fact, the distance to the Moon is less than to the Sun, almost 400 times, and not 19. His mistake is that it is impossible to accurately determine the moment when the Moon is at the top of the right angle, only on the basis of observations. He couldn’t know it yet. The slightest inaccuracy entails a huge deviation from the true value.
The greatest astronomer of antiquity Hipparchus of Nicaea in the middle of the II century BC. e. with great certainty determined the distance to the moon and its dimensions, taking the radius of the globe as a unit. In his calculations, Hipparchus proceeded from a correct understanding of the cause of lunar eclipses: the moon falls into the earth’s shadow, which has the shape of a cone with a vertex located somewhere in the direction of the moon.
The figure shows the position of the Sun, Earth and Moon during a lunar eclipse. From the similarity of triangles it follows that the distance from the Earth to the Sun AB is as many times greater than the distance from the Earth to the Moon BC, how many times the difference in the radii of the Sun and the Earth (AE – BF) is greater than the difference in the radii of the Earth and its shadow at the distance of the Moon (BF – CG ).
From observations with the simplest goniometric instruments, it followed that the radius of the Moon is 15′, and the radius of the shadow is approximately 40′, that is, the radius of the shadow is almost 2.7 times greater than the radius of the Moon. Taking the distance from the Earth to the Sun as unity, it was possible to establish that the radius of the Moon is almost 3.5 times less than the radius of the Earth.
Then it was already known that at an angle of 1′ an object is observed, the distance to which exceeds its dimensions by 3,483 times. Therefore, Hipparchus reasoned, at an angle of 15′ the observed object would be 15 times closer. This means that the Moon is at a distance from us, 3483:15 = 230 times its radius. And if the radius of the Earth is approximately 3.5 radii of the Moon, then the distance to the Moon is 230 : 3.5 ~ 60 radii of the Earth, or about 30 Earth diameters. This is about 382 thousand kilometers.
Giparchus of Nicaea received a relatively accurate distance to the moon.
How is distance measured now?
Now the distance to the Moon can be calculated with an accuracy of a few millimeters. It is enough for scientists to detect how long it takes for a laser beam launched from the Earth to reach a special reflector installed on the Moon and return back.
Soviet lunar rovers and American astronauts placed several corner reflectors on the surface of the Moon.
What it is?
Laser beams directed from the Earth to the Moon and returned by reflectors make it possible to measure the distance to the nearest millimeter. Even though only a small fraction of the 100 quadrillion laser photons sent back to Earth are enough to accurately calculate the distance.
The speed of light is almost 300,000 km/s, and it takes a little over a second for a laser beam to travel to the moon and back. Based on precisely recorded time, astronomers can easily determine the current distance to the Moon with high accuracy.
The moon is moving away
Using this method of calculating the distance, it was found that the Moon moves away from the Earth by 3.8 cm every year. This means that in millions of years the Moon will appear smaller in the sky. In a billion years, it will even appear smaller than the Sun, and total solar eclipses will become a thing of the past.
The data also helped reveal imperfections in the moon’s rotation around its axis due to the effects of Earth’s gravity. The moon has a slightly elongated orbit and shows little wiggles called librations. These wiggles indicate the presence of a viscous molten substance inside the Moon. Particularly valuable data on librations is obtained using a corner reflector located in the place where librations are most noticeable.
Image credit:
https://currentaffairs.adda247.com
https://allforchildren.ru
https://en.wikipedia.org